yogabuch / bewegungsphysiologie / gelenkformen

Gelenkformen

Ein Gelenk hat in Abhängigkeit von seiner geometrischen Form eine oder mehrere physiologische Bewegungsdimensionen, die durch Drehachsen beschrieben werden können. Die bekannten Formen der Gelenke sind mit Angabe der Bewungsdimensionen.

Kugelgelenk . Eigelenk . Scharniergelenk . Radgelenk . Sattelgelenk . Planes Gelenk

Kugelgelenk / Ball-and-Socket-Joint / Articulatio sphaeroidea

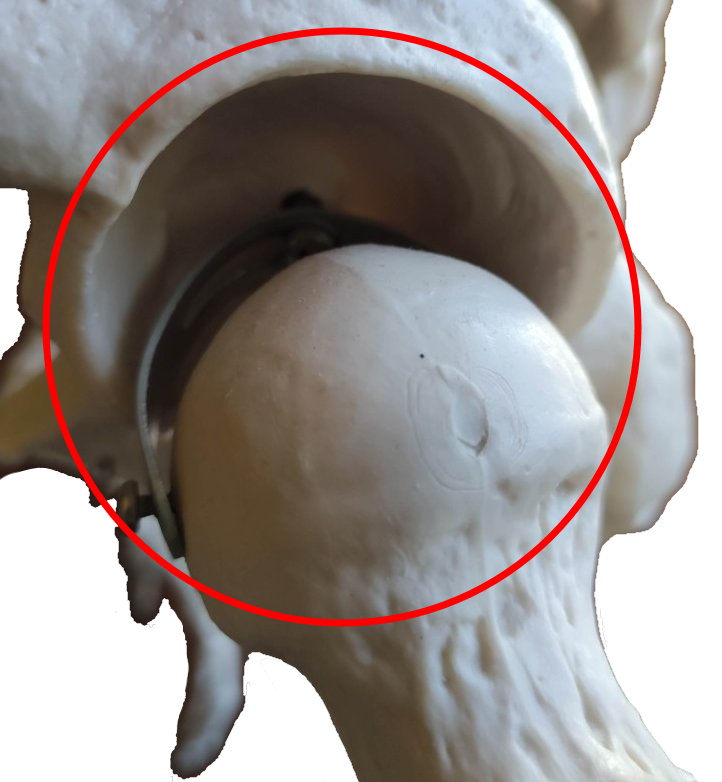
Bewegungsdimensionen: 3. Ein Kugelabschnitt greift in das kongruente konkave Gegenüber ein. Möglich sind zweidimensionales Kippen und axiale Rotation. Ein Beispiel ist das Schultergelenk. Das Hüftgelenk mit einer weiteren Umfassung stellt einen Sonderfall eines Kugelgelenks dar und wird als Nussgelenks (Enarthrosis) bezeichnet.

Eigelenk / Ellipsoid Joint / Articulatio ellipsoidea

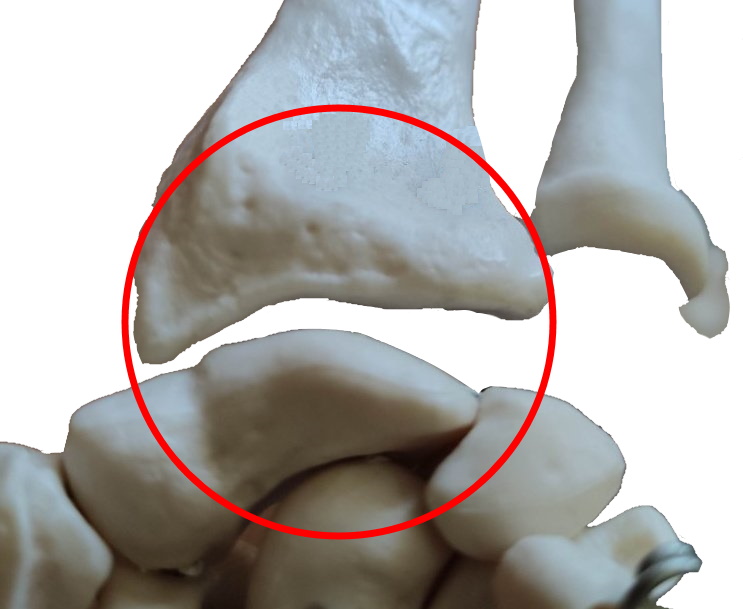
Bewegungsdimensionen: 2. Ein Ellipsoidabschnitt greift in das kongruente konkave Gegenüber ein. Möglich sind zweidimensionales Kippen, aber keine axiale Rotation. Ein wichtiges Beispiel ist das Radiokarpalgelenk.

Scharniergelenk / Hinge Joint

Bewegungsdimensionen: 1. Ein Zylinderabschnitt greift in sein kongruentes konkaves Gegenüber ein: Möglich ist nur die Rotation um die Längsachse des Zylinders. Ein wichtiges Beispiel ist das Humeroulnargelenk, also der Teil des Ellbogengelenks, in dem sich die Ulna um den distalen Humerus bewegt.

Rad- oder Zapfengelenk / Drehgelenk

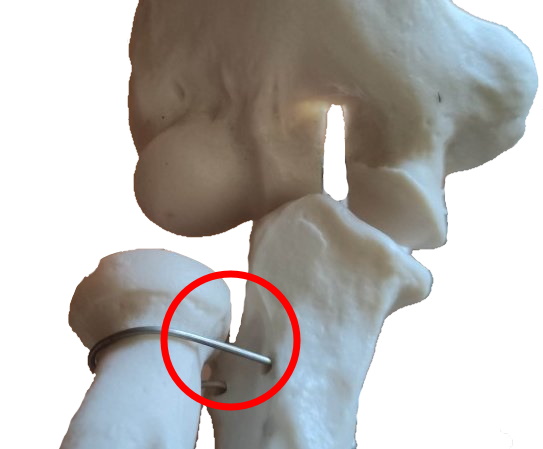
Bewegungsdimensionen: 1. Ein Zylinder greift in eine kongruentee hohlzylindrische Fläche ein: Möglich ist nur die Rotation um die Längsachse des Zylinders. Ein wichtiges Beispiel für ein Radgelenk ist das distale Radioulnargelenk, während das proximale Radioulnargelenk ein Zapfengelenk ist. Das Gelenk zwischen Atlas unsd Axis ist ebenfalls ein Drehgelenk.

Sattelelenk / Saddle Joint / Articulatio sellaris

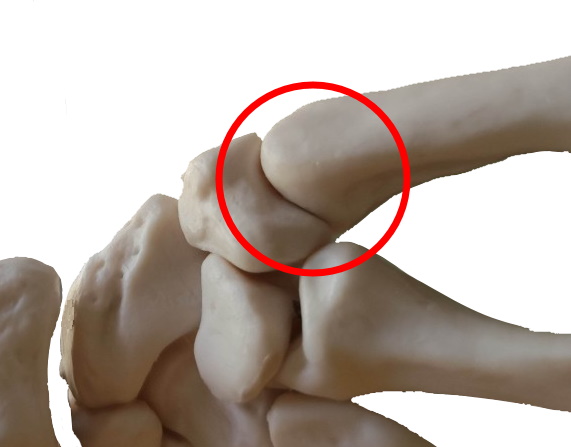
Bewegungsdimensionen: 2. Ein Sattel greift in einen 90° dazu rotierten Sattel ein: Möglich ist das zweidimensionale Kippen, aber keine Rotation. Ein wichtiges Beispiel ist das Daumensattelgelenk (Art. carpometacarpalis pollicis). Die Carpometacarpalgelenke sind ebenfalls Sattelgelenke.

Planes Gelenk / Plane Joint

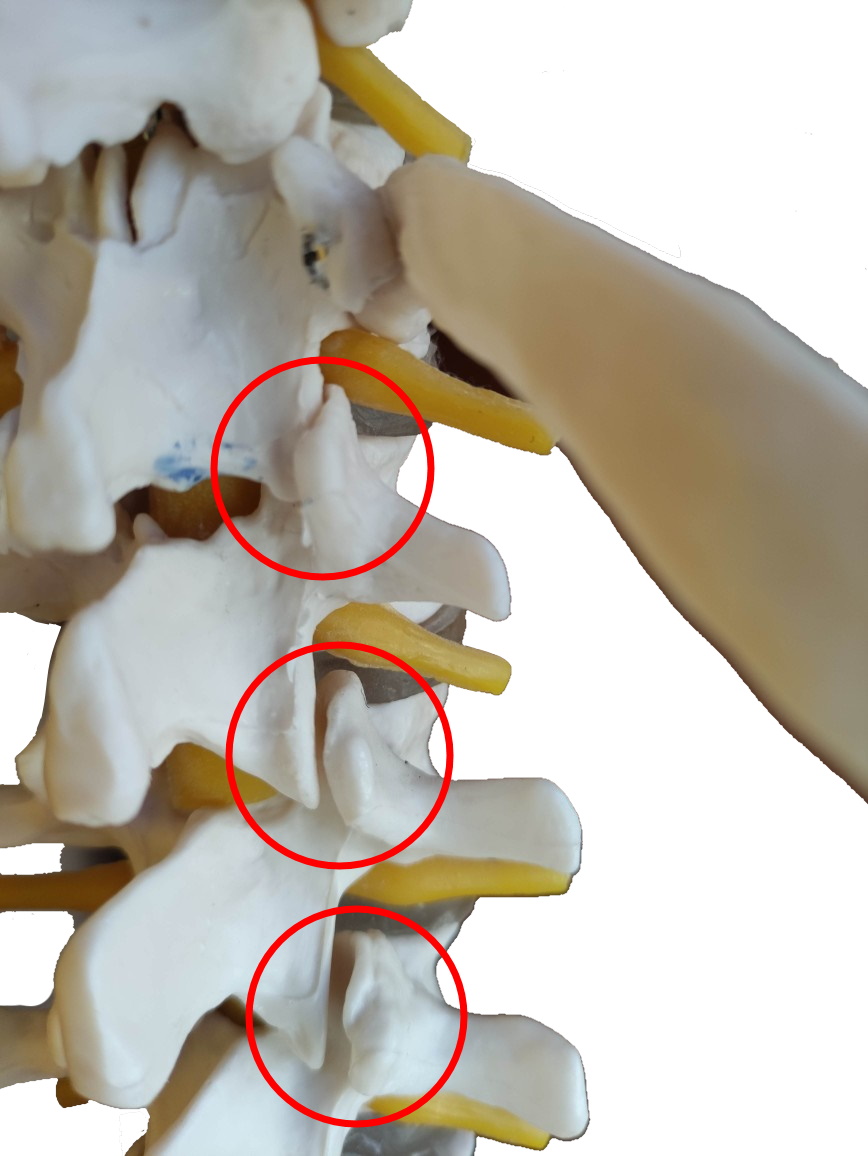
Bewegungsdimensionen: 1. Eine plane Fläche setzt auf einem planen Gegenüber auf: Möglich ist nur die axiale Rotation. Ein wichtiges Beispiel sind die Facettengelenke der Wirbelsäule.

Condylen-Gelenk

Condylen-Gelenk / Articulatio bicondylaris (2): Die Condylen der Gelenkpartner stehen in einem Winkel zueinander und erlauben sowohl eine Rotation um eine Achse durch die Condylen eines der beiden Partner (Flexion/Extension) als auch eine axiale Rotation (Endorotation/Exorotation). Ein wichtiges Beispiel ist natürlich das Kniegelenk.

Die Bewegungen der Gelenkflächen sind Abrollen oder Gleiten. Das Gleiten kann sowohl auf einer planen als auch auf einer gebogenen Fläche geschehen. Im Falle des Hüftgelenks etwa bestehen alle Bewegungen aus Gleitbewegungen. Die Kongruenz der Gelenkflächen bedeutet, daß die Radien der Krümmung übereinstimmen. Viele Gelenke sind physiologisch aber nicht zu 100% kongruent, da eine minimal kleiner Radius der Kugel, des Eis oder des Zylinders nicht nur die Beweglichkeit erhöht, sondern auch die Schmierung verbessert. Rollen und Gleiten schließen sich nicht aus, das beste Beispiel dafür ist das Kniegelenk, das eine überwiegende Rollbewegung, aber ab einem Flexionswinkel von rund 90° überwiegend eine Gleitbewegung ausführt. Darüberhinaus ist die Schlussrotation eine reine Gleitbewegung.